[프로그래머스] 게임 맵 최단거리

1. 문제

프로그래머스

2. 핵심 아이디어

BFS

3. 코드

[swift]

import Foundation

func solution(_ maps: [[Int]]) -> Int {
    var maps = maps
    let n = maps[0].count
    let m = maps.count
    let dx: [Int] = [0,0,-1,1]
    let dy: [Int] = [1,-1,0,0]
    var queue: [(Int, Int)] = []
    queue.append((0,0))
    maps[0][0] = 1
    while !queue.isEmpty {
        let element = queue.removeFirst()
        let x = element.0
        let y = element.1
        for i in 0...3 {
            let dx = x + dx[i]
            let dy = y + dy[i]
            if dx >= 0 && dx < n && dy >= 0 && dy < m {
                if maps[dy][dx] == 0 {
                    continue
                }
                if maps[dy][dx] == 1 {
                    maps[dy][dx] = maps[y][x] + 1
                    queue.append((dx,dy))
                }
            }
        }
    }
    return maps[maps.endIndex - 1][maps.endIndex - 1] == 1 ? -1 : maps[maps.endIndex - 1][maps.endIndex - 1]
}

[python]

from collections import deque

def solution(maps):
    n = len(maps[0])
    m = len(maps)
    direction = [(0,1), (0,-1), (1,0), (-1,0)]
    dq = deque()
    dq.append((0,0))
    maps[0][0] = 1
    while dq:
        x,y = dq.popleft()
        for direct in direction:
            dx = x + direct[0]
            dy = y + direct[1]
            if 0 <= dx < n and 0 <= dy < m:
                if maps[dy][dx] == 0:
                    continue
                if maps[dy][dx] == 1:
                    maps[dy][dx] = maps[y][x] + 1
                    dq.append((dx,dy))
    return maps[-1][-1] if maps[-1][-1] != 1 else -1

4. 풀이 과정

흔히 보던 BFS/DFS 탐색 문제였다!

BFS로 아직 탐색하지 않은 경로 (maps[dx][dy] == 1 인 경우) 와 벽을 피해주면서 탐색하면 되었다.

그렇게 쉽게 문제를 푼 다음, DFS로도 문제를 풀어보려 했었는데…

DFS 로는 문제가 풀리지 않았다.

[python]

def solution(maps):
    n = len(maps[0])
    m = len(maps)
    direction = [(0,1), (0,-1), (1,0), (-1,0)]
    def DFS(x,y):
        if x == n - 1 and y == m - 1:
            return
        for direct in direction:
            dx = x + direct[0]
            dy = y + direct[1]
            if 0 <= dx < n and 0 <= dy < m:
                if maps[dy][dx] == 0:
                    continue
                if maps[dy][dx] == 1 or maps[y][x] + 1 < maps[dy][dx]:
                    maps[dy][dx] = maps[y][x] + 1
                    DFS(dx,dy)
    DFS(0,0)
    return maps[-1][-1] if maps[-1][-1] != 1 else -1

이 DFS 코드가 실패하는 이유는 탐색하는 경로가 너무나 많아지기 때문이다.

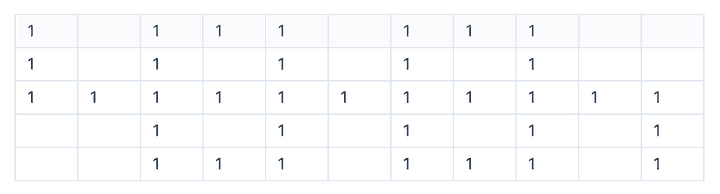
이런 형태의 맵이 있다고 가정한다면,

DFS는 교차로 (위, 오른쪽, 아래쪽) 를 모두 3^n * k (n는 삼거리의 개수, k는 삼거리의 경로 개수) 연산으로 탐색을 해야하기 때문에… 시간복잡도가 망하는 것이였다.

이처럼 문제에서 최단 거리를 제공한다면 (마지막 종착지가 정해져있고 가중치가 없음) BFS가 확실히 좋은 선택이다 라고 느꼈다.

1. 문제
2. 핵심 아이디어
3. 코드
4. 풀이 과정